情報通信研究機構(以下NICT)の成瀬 誠主任研究員、埼玉大学大学院理工学研究科の内田 淳史教授、慶應義塾大学大学院政策・メディア研究科 金 成主特任准教授らは、半導体レーザーから生じる光カオス(以下レーザーカオス)により発生した乱数を利用して、適応速度1GHzの学習に世界で初めて成功しました。
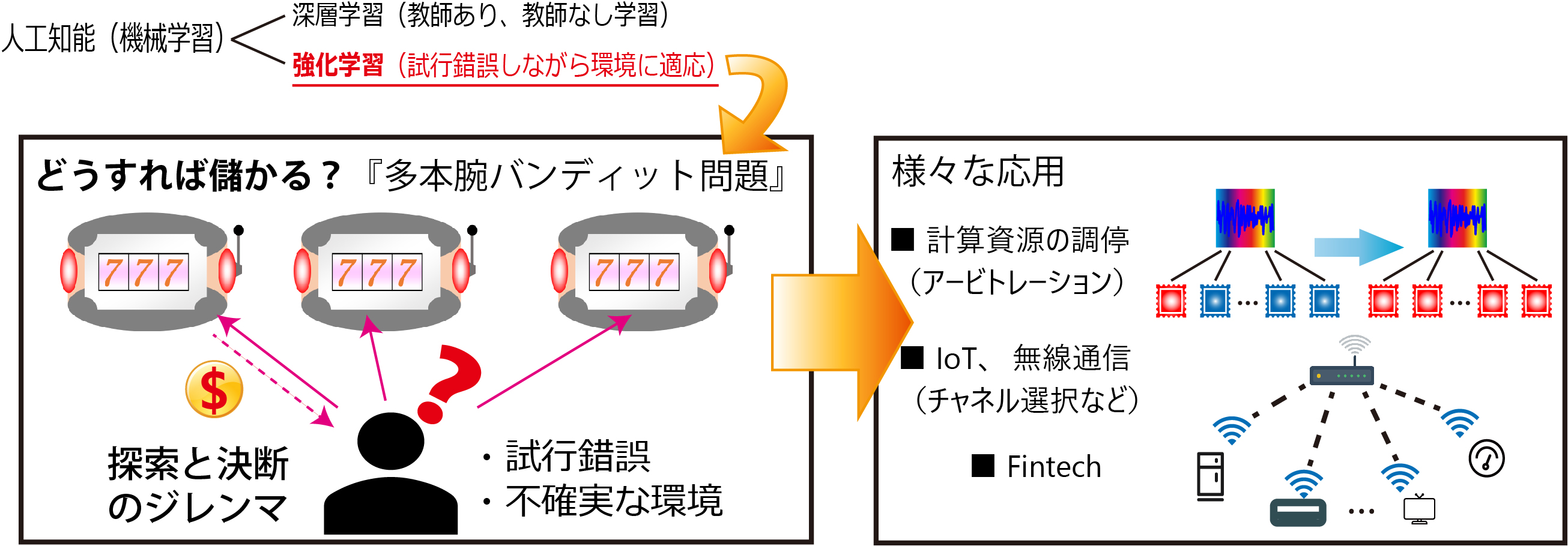
今回解いた問題:多本腕バンディット問題
強化学習は、未知の環境で試行錯誤を行いながら学習を行う方法です。今回解かれた「多本腕バンディット問題」は、「多数のスロットマシンが並んだカジノで儲けを最大にするためにどのようにすえばよいか?」を決める問題です。試し打ち=あたり台を見つけるための試行は、多すぎれば試し打ちだけで損をしてしまうし、少なすぎてはあたり台を見つけ損なう可能性もあります。また、あたり台が常に一定とは限りません。
このような「探索」と「決断」にジレンマが存在するような問題としては、ワイヤレス通信における周波数の割当て、データセンターでの計算資源の割当て、ロボット制御、Web広告などがあります。
高速な試行=高速な乱数発生
強化学習では、試行=入力信号の発生に乱数を用います。乱数の質が良く、発生速度が速いほど、短時間に多くの試行が可能になります。従来の強化学習で用いられていた疑似乱数は、コンピュータ上でアルゴリズムによって生成されるため、その速度には限界があり、また予測不可能性の点でも限界があります。
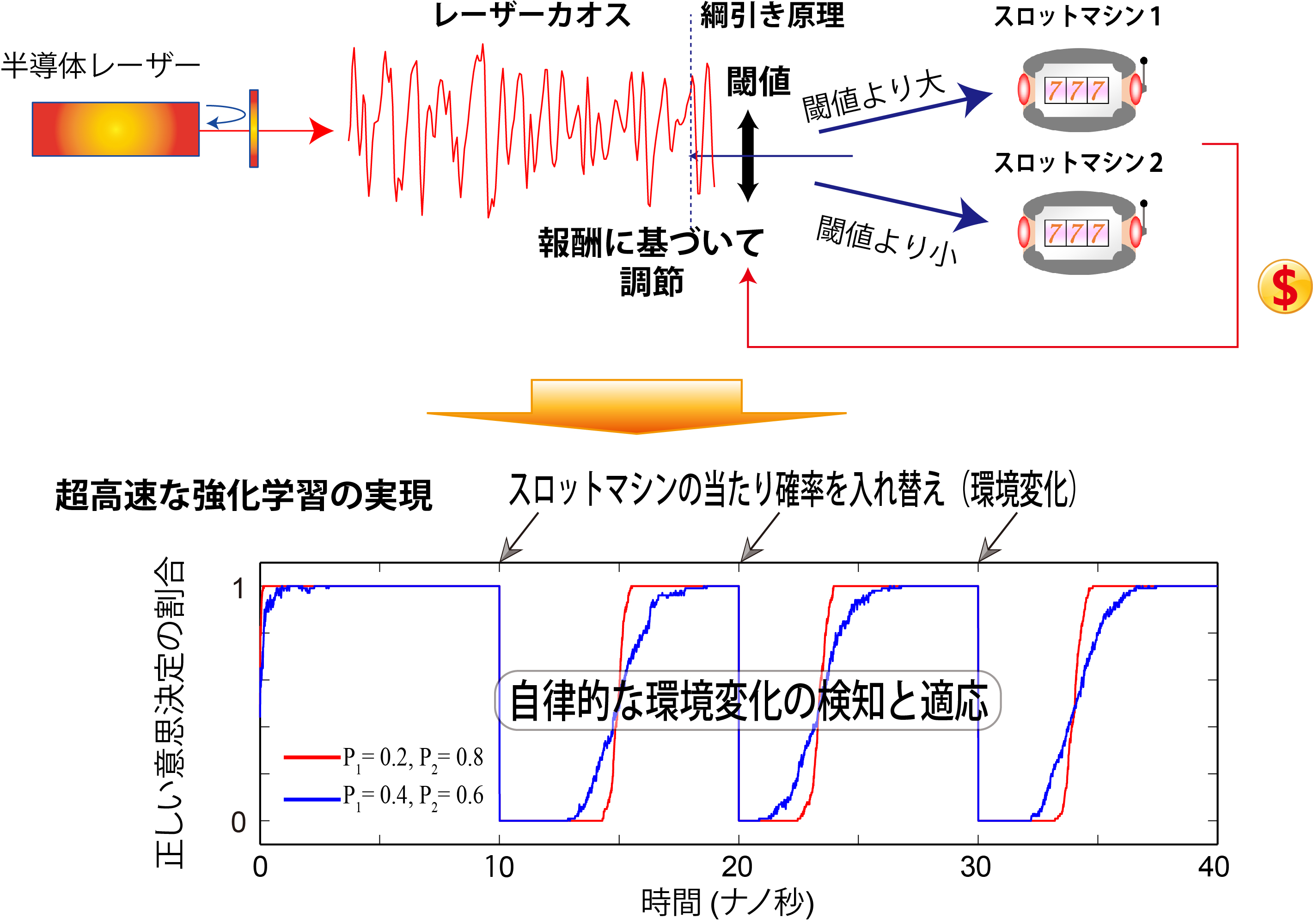
今回利用された「レーザーカオス」は、半導体レーザーの出力光を反射鏡によってレーザーに戻すことでレーザーが不安定になり出力される光の強度がランダムに変動する「戻り光レーザーカオス」と呼ばれる現象です。予測不可能性に優れておりかつ高速な乱数生成が可能にいなることで、注目されています。
綱引き原理による学習
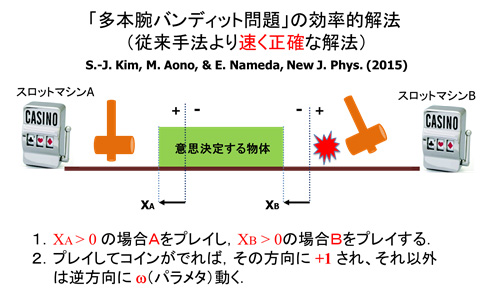
今回の研究では、レーザーカオスを用いて、2台のスロットマシン(スロットマシン1、スロットマシン2)からあたり台を見つけるために、レーザーカオス光を1秒間に最大1000億回サンプリングして、設定した「閾値」との大小判定で意思決定を行いました。学習は「閾値」を「過去の戦績」に基づき上下する、「綱引き原理」と呼ばれる独自の方式を用いています。
綱引き原理は、今回の研究に参加している金成主氏が発見した手法で、粘菌のふるまいから抽出した意思決定原理です。
参照情報:効率的に試行錯誤する方法 – 意思決定の物理原理 -(理科学研究所)
2017年2月には、金氏らが参加する自然知能グループで、アンスティチュ・フランセ東京で開催されたイベント「Digital Choc 2017—欲望する機械」に、インスタレーション「棒知能(Bar Intelligence 01)」を出展しています。
低レイテンシーでの強化学習、環境変化にも適応
結果、50ピコ秒間隔(毎秒200億回)のサンプリングでの試行が最も適応性に優れており、20回の試行(1ナノ秒)で9割以上の正解が得られました。また、10ナノ秒ごとに行われたあたり台の入れ替えにも、入れ替え直後に意思決定の性能が一旦劣化し、その後自律的に回復する「不確実な環境における適応」が見られました。
強化学習のボトルネックを解消
高速な物理乱数が利用できることで、従来技術では不可能だった高速化が可能になることが期待されます。また、フォトニクスを利用することで、安定性や集積性に優れたシステムの実現が可能になります。応用面では、フィンテックにおける超高速取引での意思決定やシステムのアービトレーション技術への応用が期待できます。
実用化にあたってはレーザーカオス光を用いた乱数発生器の小型化が課題となりますが、金沢大学の砂田 哲氏は二次元共振器構造で230μm× 1 mmの大きさのレーザーカオスデバイスの試作に成功しています。(「高速物理乱数生成を可能にする微小レーザカオスデバイスの研究」砂田 哲、電気通信普及財団 研究調査報告書 No.29 2014 )スマートフォンや各種デバイスへの搭載への可能性も見えてきています。